437. 路径总和 III

Similar Question

leading to the advanced question

Solution Tips

方案一: 双重递归

var pathSum = function (root, targetSum) {
    if (root === null) return 0
    let path = 0
    dfs(root, sum)

    return path
    // 前序遍历每个节点，对每个节点调用acc函数
    function dfs(node, sum) {
        if (node === null) return
        acc(node, sum, 0)
        dfs(node.left, sum)
        dfs(node.right, sum)
    }
    // 计算以当前节点为起点的路径是否存在符合题意的 case
    function acc(node, sum, cur) {
        if (node === null) return

        cur += node.val
        if (cur === sum) path++

        acc(node.left, sum, cur)
        acc(node.right, sum, cur)
    }
};

方案二: 前缀和

这道题我们可以使用前缀和来求解，比如，给定数据为：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8，对应的二叉树及其前缀和为：

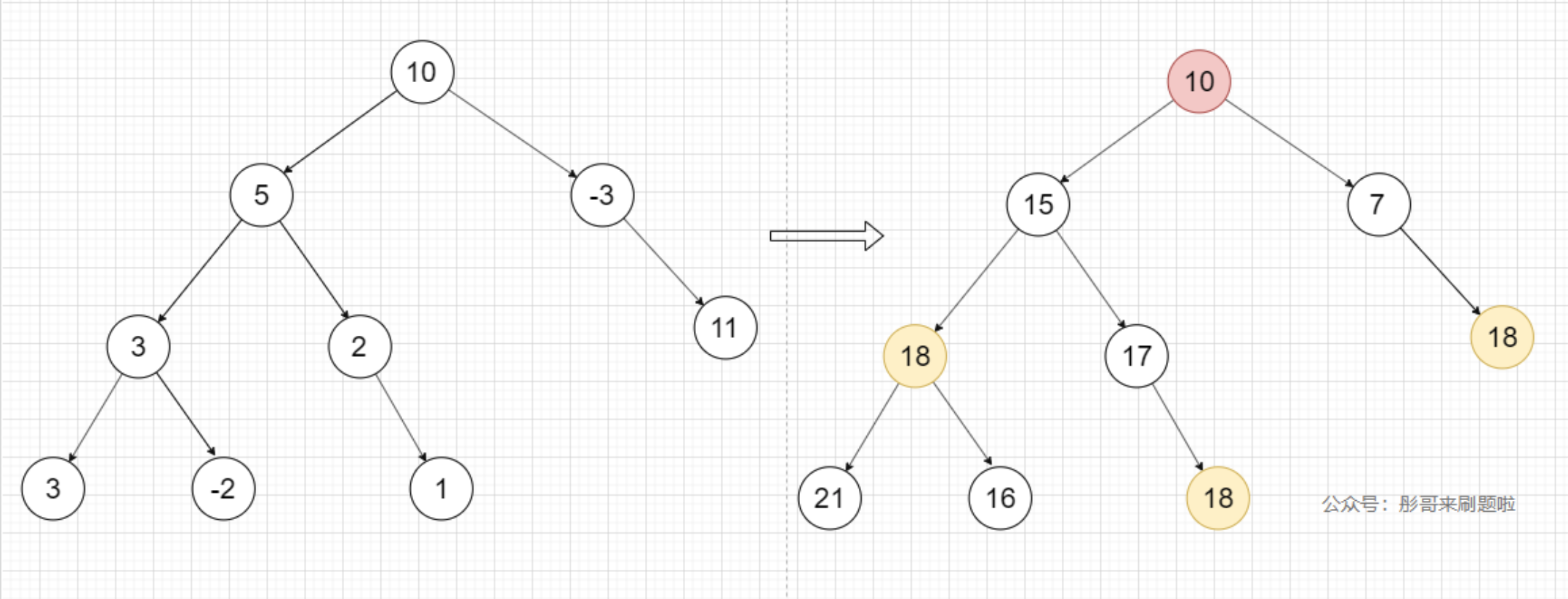
有了前缀和，我们只要在每一条路径上求解：两个节点之差等于 targetSum，即可。

为了更快速的找到某个数值在路径中是否出现过，我们可以使用哈希表记录路径中每个数值出现的次数，比如，上图中哈希表中记录了 10 这个数值，当遍历到 18 时，发现哈希表中有 18 - 8 = 10，总次数加上 10 出现的次数即可。

另外，为了处理包含根节点的情况，我们需要在哈希表中存储一个 (0,1) 的键值对。

而且，我们并不需要一开始就把前缀和树计算出来，我们可以边遍历边计算，这里使用回溯来处理。

var pathSum = function(root, targetSum) {
  const prefix = new Map();
  prefix.set(0, 1);
  return dfs(root, prefix, 0, targetSum);
}

const dfs = (root, prefix, curr, targetSum) => {
  if (root == null) {
      return 0;
  }

  let ret = 0;
  curr += root.val;

  ret = prefix.get(curr - targetSum) || 0;
  prefix.set(curr, (prefix.get(curr) || 0) + 1);
  ret += dfs(root.left, prefix, curr, targetSum);
  ret += dfs(root.right, prefix, curr, targetSum);
  prefix.set(curr, (prefix.get(curr) || 0) - 1);

  return ret;
}